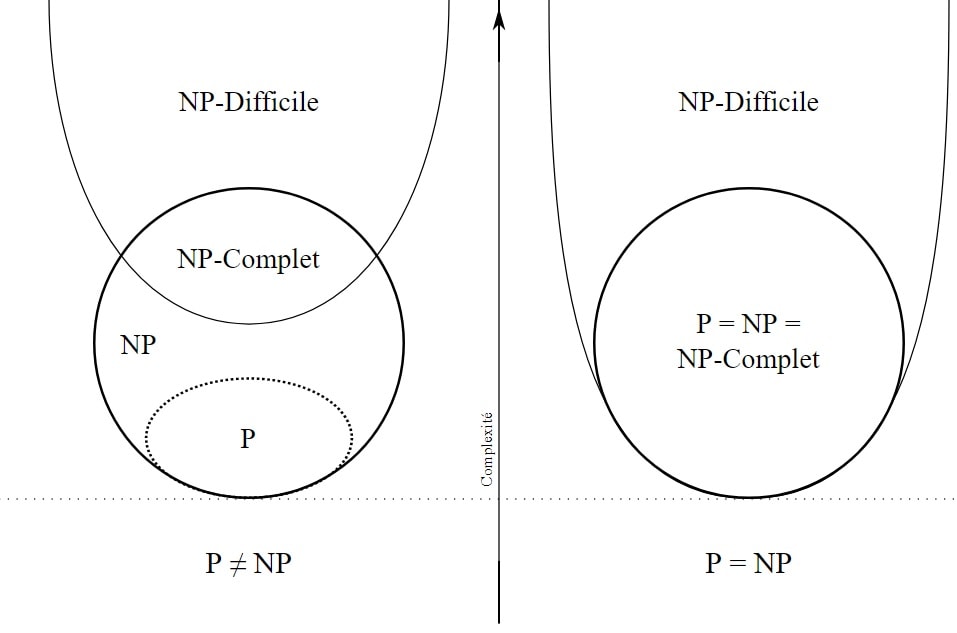
Depuis notre enfance nous avons continuelle appris des techniques et principes mathématiques plus ou moins abstraites qui nous permettent quotidiennement de résoudre certains problèmes. Exemple : les systèmes d’équations et inéquations nous permettent au quotidien de résoudre des problèmes à plusieurs variantes, de trouver les solutions de certaines opérations rapidement grâce aux algorithmes implémentés dans les machines à calculer. Cependant, il existe un certain nombre de problèmes dont la résolution passe par un processus long et fastidieux (NP) et d’autres dont la résolution est rapide ou évidente(P).
L’un des problèmes du millénaire est de pouvoir démontrer que tout problème NP peut avoir une solution évidente P.
Un exemple contrait est le suivant :
“Supposons que vous organisiez des logements pour un groupe de quatre cents étudiants universitaires. Les places sont limitées et seulement une centaine d’étudiants recevront des places dans le dortoir. Pour compliquer les choses, le doyen vous a fourni une liste de paires d’étudiants incompatibles et a demandé qu’aucune paire de cette liste ne figure dans votre choix final. C’est un exemple de ce que les informaticiens appellent un problème de NP car il est facile de vérifier si un choix donné de cent étudiants proposés par un collègue est satisfaisant (c’est-à-dire qu’aucun couple pris sur la liste de votre collègue ne figure également sur la liste de bureau du doyen), cependant, la tâche de générer une telle liste à partir de zéro semble être si difficile qu’elle est tout à fait irréaliste. En effet, le nombre total de façons de choisir cent étudiants parmi les quatre cents candidats est supérieur au nombre d’atomes dans l’univers connu ! Ainsi, aucune civilisation future ne pourrait jamais espérer construire un supercalculateur capable de résoudre le problème par la force brut ; c’est-à-dire en vérifiant chaque combinaison possible de 100 étudiants. Cependant, cette difficulté apparente ne peut que refléter le manque d’ingéniosité de votre programmeur.”
En fait, l’un des problèmes en suspens en informatique consiste à déterminer s’il existe des questions dont la réponse peut être vérifiée rapidement, mais qui nécessitent un temps incroyablement long pour être résolues par une procédure directe. Des problèmes comme celui mentionné ci-dessus semblent certes être de ce type, mais jusqu’à présent, personne n’a réussi à prouver qu’aucun d’entre eux est vraiment aussi difficile qu’il y paraît, c’est-à-dire qu’il n’y a vraiment aucun moyen possible de générer une réponse avec l’aide d’un ordinateur. Stephen Cook et Leonid Levin ont formulé le problème P (c.-à-d. Facile à trouver) par opposition à NP (c.-à-d., Facile à vérifier mais difficile à réaliser) indépendamment en 1971.
Donc si vous réussissez à prouver que tous les problèmes NP ont une solution P, vous aurez résolu l’un des plus grands problèmes du monde moderne et aider considérablement à l’évolution de la civilisation humaine tout en empochant une maudite somme d’un million de Dollars.
La résolution du problème P=NP permettrait par exemple à un ordinateur de résoudre un Sudoku en quelque seconde, de miner facilement la cryptomonnaie ou d’effectuer les opérations de grande échelle en un temps record.
Si par chance vous réussissez à résoudre ce problème n’oubliez pas de m’inviter le jour de la remise de vos 1 million ??.
